はじめに

こんにちは、中村です。機械学習が扱う様々なタスクの中に、複数の予測を同時に要求されるタスクがあります。例えば、複数の候補をユーザに提示する検索や推薦は、これに該当すると考えることができます。一般的には、候補のスコアに基づくランキングを利用する形で複数の予測を得ることができます。

今回は特殊なケースとして、予測の数がkに固定されている状況を考えます。ランキングが得られていれば上位k個を選択するだけで簡単に要件を満たせます。一方で、そもそもk個返すことが決まっているのなら候補をk個選択するための学習を考えてみたくなります。

本記事では候補の集合から上位k個を選択する問題(top-k選択問題)について、ディープラーニングを用いたアプローチをいくつか紹介します。

はじめに
微分可能top-k選択
top-k選択の応用
まとめ

微分可能top-k選択

top-k選択問題にディープラーニングで迫ると大きな困難に阻まれます。 k個を選択する操作が不連続であり、勾配を計算できないため、そのままでは勾配法によるend-to-endな学習ができません。

top-k選択操作を微分可能とするために一定の支持を得ているのが連続緩和や平滑化と呼ばれるテクニックです。一般的な分類問題(top-1選択問題)においてone-hotベクトルをsoftmax関数で近似するように、top-k選択操作の表現であるk-hotベクトルについて、その算出を連続な関数で記述することにより勾配を計算できるようになります。

top-k選択の平滑化は複数の提案が存在しているようです。以降では次の3つのアプローチを取り上げ、それぞれの考え方を整理します。本記事では概要に触れるだけに留め、それぞれあまり深く掘り下げません。

Gumbel-max trickの拡張
最適輸送による定式化
Hinge関数を使った損失関数の平滑化

1.と2.はオペレータの提案です。ネットワークの途中に組み込むことでtop-k選択モジュールとして機能します。3.は損失関数の提案です。出力の上位k個を評価する際に使います。

以降の説明では度々スコアという用語が登場しますが、これを予測の候補に付与された数値を指す語として統一します。一般的な分類モデルにおける最終層の出力をイメージしていただければわかりやすいと思います。本記事が紹介する手法はすべてスコアが入力になっています。

Gumbel-max trickの拡張 [Xie and Ermon, 2019]

Weighted Reservoir Sampling(WRS)は要素数nの集合からk個の要素を重複なくランダムに取得するアルゴリズムです。 [Efraimidis and Spirakis, 2006]の実装では、各要素がrandom keyと呼ばれる値を持ち、random keyが大きい順に要素が選択されます。ここで、random keyの値は一様乱数と各要素のスコアで決まります。random keyを $\ \mathbf{r}=[r_1,\ldots,r_n$ ]とします。

WRSをreparameterization trickと連続緩和によって微分可能としたことが[Xie and Ermon, 2019]の貢献です。

まず、random keyの計算にはGumbel-max trickが用いられます。ここでやりたいことは決定的な変換とランダム性の分離です。実装は簡単で、スコアベクトルにGumbel分布からの乱数を足すだけです。

続いてtop-k選択を微分可能なアルゴリズムに落とし込みます。WRSの出力はk-hotベクトルですが、ここでは緩和されたk-hotベクトル $\mathbf{a}=[a_1,\dots,a_n$ ]を考えます。 $\sum_{i=1}^{n} a_i=k$ であり、 $0 \leq a_i \leq 1$ です。要素を1個選択する操作はsoftmax関数で記述できます。random key $\mathbf{r}$ をロジットと見れば、 $\text{softmax}(\mathbf{r})$ は緩和されたone-hotベクトルを出力します。要素をk個選択する操作は、同じ操作をk回実行すれば達成されます。ただし、 $\mathbf{r}$ を再利用すると毎回同じ要素が選択されてしまいます。そこで、一度選択された要素に対応するrandom keyはマスクすることで重複を回避します。

この工程は実際に実装を参照するほうが理解の助けとなるかもしれません。

def relaxed_wrs(score, top_k, temperature=1.0, eps=1e-10):
    u = torch.rand(score.size())
    g = -torch.log(-torch.log(u + eps) + eps)
    random_keys = score + g

    soft_khot = torch.zeros_like(score)
    soft_onehot = torch.zeros_like(score)
    for i in range(top_k):
        mask = F.relu(1 - soft_onehot)
        random_keys = random_keys + torch.log(mask + eps)
        soft_onehot = F.softmax(random_keys / temperature, dim=1)
        soft_khot = soft_khot + soft_onehot
    return soft_khot

最適輸送による定式化 [Petersen+, 2022]

top-k選択を、n個の要素を0か1のどちらかに割り当てる操作として考えます。スコアの上位k個を1に割り当て、残りのn-k個を0に割り当てればtop-k選択と同じ結果を得ることができます。図は $k=2$ の時の様子を示しています。

(https://arxiv.org/abs/2002.06504)

これを輸送問題として定式化すると以下になります。

$\displaystyle \Gamma^\star = \arg\min_{\Gamma \geq 0} < C, \Gamma > \ \ \ s.t. \ \ \Gamma \boldsymbol{\mathbb{1}}_{m}=\mu, \ \Gamma^\top\boldsymbol{\mathbb{1}}_{n}=\nu$

$\Gamma \in \mathbb{R}^{n \times m}$ は輸送量(割り当てのプラン)、 $C \in \mathbb{R}^{n \times m}$ はコスト行列です。各要素の割り当てにそのコストを掛けた量を最小化する問題です。今回は $\left\{0,1\right\}$ への割り当てを解くので $m=2$ 、コスト行列は、例えば $\left\{0,1\right\}$ までのユークリッド距離( $C_{i1}=s_i^2, C_{i2}=(s_i-1)^2$ )が使えます。制約条件はすべての要素が抜け漏れなく0か1のどちらかに対応するように強制するもので、 $\mu=\boldsymbol{\mathbb{1}}_{n}/n, \nu=\left[k/n, (n-k)/n\right]$ とします。

最適な輸送量 $\Gamma^\star$ からtop-k選択のためのオペレータ $A$ が得られます。これはtop-kの要素を示すk-hotベクトルになっています。

$\displaystyle A = n\Gamma^\star \cdot \left[ 1, 0 \right]^\top$

元々の輸送問題は不連続なためこのままでは学習に適しません。そこで、エントロピー正則化による連続緩和を試みます。

$\displaystyle \Gamma^{\star,\epsilon} = \arg\min_{\Gamma \geq 0} < C, \Gamma > + \epsilon H(\Gamma) \ \ \ s.t. \ \ \Gamma \boldsymbol{\mathbb{1}}_{m}=\mu, \ \Gamma^\top\boldsymbol{\mathbb{1}}_{n}=\nu$

ここで、 $H(\Gamma)=\sum_{i,j}\Gamma_{ij} \log \Gamma_{ij}$ です。この緩和により、 $\Gamma$ は密行列となり、今回の目的である $A^\epsilon = n\Gamma^{\star,\epsilon} \cdot \left[1,0\right]^\top$ はソフトなk-hotベクトルとなります。

$\Gamma^{\star,\epsilon}$ はSinkhornアルゴリズムを使って反復的に計算できます。Sinkhornアルゴリズムの詳細はこちらの資料がとても参考になります。 $\Gamma^{\star,\epsilon}$ を得るまでの工程で不連続性が排除されているため、top-k選択操作全体が微分可能となります。

Hinge関数を使った損失関数の平滑化 [Garcin+, 2022]

ここまではスコアベクトルをソフトなk-hotベクトルに変換する方法をみてきましたが、これらとは別にスコアベクトルを直接評価する手法も提案されています。 Gumbel-max trickと最適輸送はk個の選択が目的でした。一方、次に紹介する手法は本来top-1予測が目的であるがk個の提案を許容されている場合を想定しています。同じtop-k問題ではありますが、立ち位置が異なることに注意が必要です。

$\mathbf{s} \in \mathbb{R}^n$ を正規化されたスコアベクトルとします。 $top_k(\mathbf{s})$ は $\mathbf{s}$ の中から $k$ 番目に大きい値を返す関数、 $s_{(k)}$ をその値、 $I[\cdot$ ]を指示関数とします。真のクラスのスコア $s_y$ がtop-kに含まれていることは以下の式で評価できます。

$\displaystyle l^k(\mathbf{s},y) = I[top_k(\mathbf{s}) > s_y$ ]

具体的に、 $n=3,k=2$ の場合、 $y=3$ が真のクラスであるとすると、 $\mathbf{s}$ の3番目の要素がtop-2に含まれていれば正解です。つまり、 $s_1 \lt s_3$ もしくは $s_2 \lt s_3$ のとき $l^k(\mathbf{s}, y)$ の値は0になり、 $s_1>s_3$ かつ $s_2>s_3$ のときは1になります。この様子は図の(a)のように表現できます。三角形の頂点がそれぞれ $\mathbf{s}=(0,0,2),(0,2,0),(2,0,0)$ を表していて、重心の下側が3番目の要素が最小となり $l^k(\mathbf{s},y)$ の値が1となる領域です。

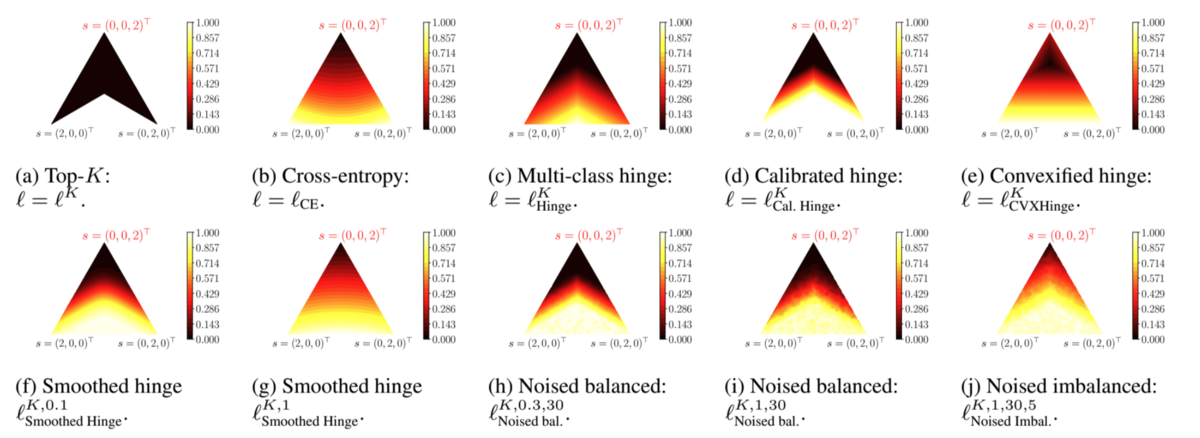
(https://arxiv.org/abs/2202.02193)

ヒンジ関数を使った緩和は例えば次の形が考えられます。

$\displaystyle l_{Hinge}^k(\mathbf{s},y) = (1 + top_k(\mathbf{s}_{\backslash y}) - s_y)_+$

$(\cdot)_+$ は $\max(0, \cdot)$ 、 $\mathbf{s}_{\backslash y}$ は $\mathbf{s}$ から $s_y$ を除いたベクトルです。この関数の様子は図の(c)に示されています。(a)と比較して、0と1の間が補間されていることが確認できます。

ちなみに $l_{Hinge}^k$ は勾配がスパースになることからうまく学習できないことが指摘されており、[Garcin+, 2022]ではこれを改善する平滑化を提案しています。

top-k選択の応用

真っ先に思いつくのは分類問題への応用です。k個の予測が許容される設定において、top-1予測のスコアのランキングを使うのではなく、k個の候補選択を直接学習します。[Petersen+, 2022]では分類問題を対象に、複数のkを同時に最適化するtop-k損失を提案しています。kに対して柔軟な学習がtop-kだけでなくtop-1の精度も改善することを主張しています。

top-k選択を組み合わせの生成技術として捉えると活用の機会は多く存在しているように感じます。[Cordonnier+, 2021]は高解像の画像に対するパッチ選択をtop-k選択オペレータで実現しています。パッチ選択が微分可能となったことで、タスクに有効な局所特徴量をダウンサンプリングを回避しながら抽出できます。論文では道路標識の認識タスクやパッチ間の関係推論タスクでパッチ選択の有効性を検証しています。

まとめ

本記事ではtop-k選択操作をニューラルネットワークで学習可能とするために提案された手法をいくつか取り上げ、緩和の適用を中心にそれぞれの考え方を整理しました。 top-k選択は、組み合わせの出力が要求される場面において、自己回帰的なアルゴリズムを置き換えて効率化できる可能性があります。実践的な応用も数多く存在しているかもしれません。

最後に、バイセルではAI技術の社会実装をリードするMLエンジニアや研究者を随時募集中です。気になる方は是非ご検討ください。

https://herp.careers/v1/buyselltech/mVOb0zUriWu8

https://herp.careers/v1/buyselltech/P_1i4hwTp63a